1. Simulating a Raman transition with constant lasers

To present the features of the package, we show the simulation of a theoretically well understood transition that takes advantage of a detuning: the Raman transition. Here, we will simulate the system with constant lasers. For laser pulses see the second tutorial.

Feel free to change parameters and play around to compare the simulation results with the theory.

from atomcalc import Level, Laser, Decay, System, plot_pulse

We define the energy levels, the decay channels (here we assume no decay), the laser parameters, and the system.

Delta is the detuning at level3 and delta is the detuning at level2 in angular frequency. The Omega are the Rabi frequencies of the corresponding lasers in angular frequency.

The detuning argument of the laser is the detuning of the laser as an angular frequency.

Using the draw function we can look at a sketch of the system.

# define level objects
level1 = Level(0)
level2 = Level(20)
level3 = Level(100)

# define decay object
decay = Decay([0,0],[[level3,level1],[level3,level2]]) # no decay
# Alternatively: decay = Decay([0],[[level3,level1]]). It needs at least one entry.

# define parameters
Delta = 20
delta = 0
Omega1 = 1
Omega2 = 1

# define lasers (sort level couples from low to high energy.)
laser1 = Laser(Omega1, Delta, [level1,level3])
laser2 = Laser(Omega2, Delta-delta, [level2,level3])

# define system (sort levels by energy in ascending order. The order of the lasers should not matter.)
system = System([level1,level2,level3], [laser1,laser2], decay)

# draw the system in matplotlib
system.draw()

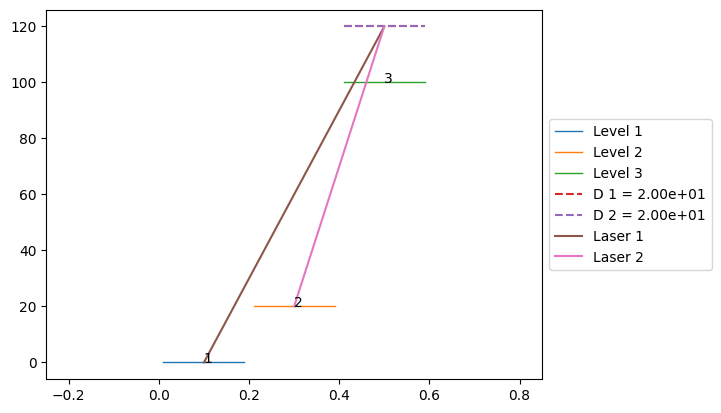
Now, we can simulate the time evolution of the level population.

Note that a laser only affects the one specific transition that it is assigned to.

# calculate and show the time evolution
system.simulate([1,0,0], 1, 300, Diagonalization=True)

Hamiltonian in the rotating frame: Quantum object: dims = [[3], [3]], shape = (3, 3), type = oper, isherm = True
Qobj data =
[[ 0.   0.   0.5]
 [ 0.   0.   0.5]
 [ 0.5  0.5 20. ]]

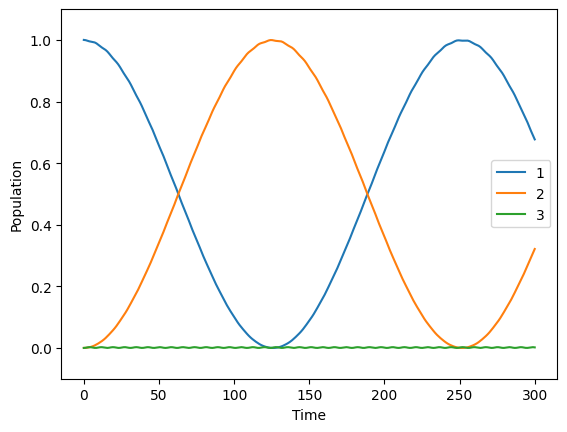
Maximum population of level 2:

0.999536989981741